頭脳王で2回も優勝したことのある河野玄斗氏が、
【裏技】三角関数の中身を簡単にずらす方法
というタイトルでYouTubeに動画をあげていました。
この動画を見た時、
遅い
と感じました(ネットワーク環境の話ではないです)。
僕が動画を見る前に想像していた方法なら、3秒どころか問題を読み終えた瞬間に答えを導けると思ったのです。
今回はその方法を解説しましょう。
【裏技】三角関数の中身を「超」簡単にずらす方法
まずは方法だけ解説して仕組みは後で解説します。方法だけだとわけがわからないかもしれませんが、ちゃんと仕組みはあります。
ではまず、河野玄斗氏が動画の最初に解いた問題、sin(x-90°)を例にとりましょう。
sin(x-90°)の例
sinなので上を向いている矢印(↑)を想像。
-90°なので上向き矢印が反時計回りに90°回転(時計回りに-90°回転)し、左向き(←)になる。
xにプラス記号が付いているので矢印そのまま(←)。
左向きは-cosxを表すので答えは-cosx
一般的な解き方
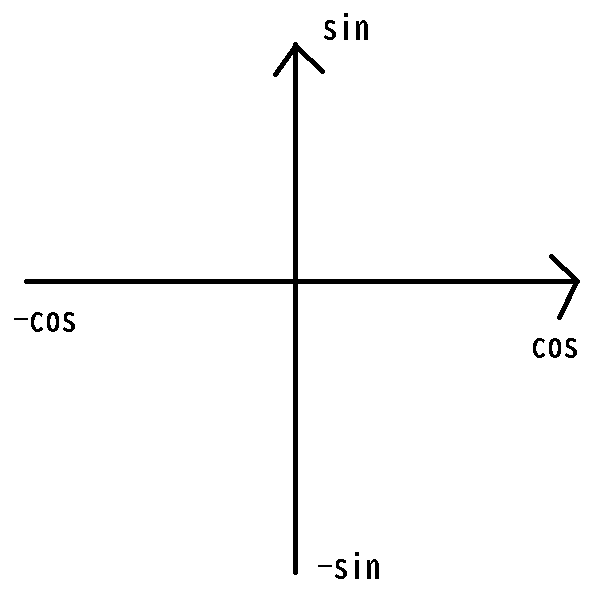
矢印という訳の分からないものが出てきましたが、それぞれの向きにcos,sin,-cos,-sinが割り振られています。
みなさんご存じのように、x軸はcos、y軸はsin、のようなところがあり、x 軸正の向き(→)がcosで負の向き(←)が-cos、y軸正の向き(↑)がsinで負の向き(↓)がsinというような割り振りになります。合理的です。
そして90°やら-180°やらと角度が出てきたら、その角度だけ時計回りに矢印を回します。
その後でxにもしマイナス符号が付いていたら矢印をx軸に対象になるようにひっくり返します。
それで最終的に向いている方向の三角関数が求めるべき答えです。
以上をまとめると、
初期の矢印の向きを判断→時計回りに回転→xにマイナス符号があったら上下反転→矢印の向きから答えを判断
ということになります。
実際に他の例やってみましょう。
cos(180°-x)の例
さっきまとめた通りの順にやります。
初期の矢印の向きを判断
cosなので右向き(→)です。
時計回りに回転
時計回りに180°回転すると、左向き(←)になります。
xにマイナス符号があったら上下反転
マイナス符号があるので上下反転しますが、左向き(←)は上下反転しても左向き(←)のままなのでやはり左向き(←)です。
矢印の向きから答えを判断
左向き(←)は-cosを表すので、答えは-cosxです。
結局仕組みは何なのか
仕組みは、単位円の軸移動です。
y=3x+5をx軸方向に4動かしてくださいと言われたときに、x軸自体を-4動かしてy=3(x-4)+5とするのと同じような仕組みです。
さきほどのcos(180°-x)を例にとりましょう。
cos(180°-x)とは、cosxの角度xに180°を加えxは負にしておく、という操作をしたものです。
これを軸だけで考えます。
xに180°を加えるということは、軸をずらすという観点からいくと、x軸とy軸を時計回りに180°回すということと同じです。
そしてxを負にするということは、単位円においてxがx軸を起点に時計回りに回転していたのが、反時計回りになるということです。これは結局、x軸に関して線対称になるということと同じです。つまり、y軸がひっくり返ります。
この操作で得られる軸の向きは次の図のようになります。

このx軸y軸の状態で、角xの位置は変わっていないですから、-cosxが答えだとわかります。
これらの操作を一瞬でできるように簡略化したのが、今回説明した方法です。
注意点
操作順序として、
初期の矢印の向きを判断→時計回りに回転→xにマイナス符号があったら上下反転→矢印の向きから答えを判断
というように説明しましたが、この順番はしっかりと守ってください。
「時計回りに回転→xにマイナス符号があったら上下反転」の順番を入れ替えると間違いになります。
例えばsin(90°-x)は答えがcosxなのですが、順番を入れ替えてしまうと-cosxという間違ったものが出てきます。
この理由は、順番を入れ替えるとsin(90°-x)ではなくsin{-(90°-x)}を計算したことになってしまうからです。
「数字から記号」の順番ですので、間違えないように注意してください。
最後に
冒頭で「問題を読み終えた瞬間に答えを導ける」と書きましたが、これは問題を読みながら考えるから読み終えた瞬間に答えが出てくるのであって、本当に一瞬で考えているわけではないです。
ただ、鍛えれば河野玄人氏の3秒を超えるくらいは余裕だとは思います。
河野玄人氏が言っていた方法は少し難しいので、どうぞこの「超」簡単な方法を試してみてください。
あ、ちなみにタンジェントの方は軸移動とか無理なのでお好みの方法でどうぞ。


コメント